항공역학 [15] 에어포일 주위의 비압축성 유동 - 얇은 에어포일 이론 (Thin Airfoil Theory)

이번 글에서는 얇은 에어포일에 대해서만 살펴볼 것이다.

 

에어포일이 매우 얇다면 캠버선을 와류면(Vortex sheet)으로 표현할 수 있기 때문에 와류면에 대한 글에서 살펴본 내용을 그대로 적용할 수 있기 때문이다.

 

그리고 에어포일 위아래면을 따라 유동이 흐른다고 가정할 것이다.

 

 

먼저 위 그림처럼 얇은 에어포일을 가정해보자.

 

y축을 따라 날개가 뻗어있는 형태이며, zx평면으로 자를 때 위 그림처럼 에어포일을 볼 수 있는 형태이다.

 

에어포일 위의 한 점의 좌표를 (x, z)로 나타낼 때 z는 x에 대한 함수라고 쓸 수 있다. 즉,

$$z=z(x)$$

 

그리고 받음각이 $\alpha$인 경우를 생각하기 위해 유동이 x축과 $\alpha$를 이룬 각도로 불어온다고 하자.

 

에어포일 위의 임의 점 P에서의 접선이 x축과 이루는 각도를 $\theta$라고 하자.

 

P에서의 캠버의 기울기가 $dz\over dx$인 것을 알고 있으므로, P에서 그을 수 있는 수직선의 기울기는 $-{dz\over dx}$임을 바로 알 수 있다.

 

그렇다면 P에서 경험하는 실질적인 받음각은 기존 받음각과 캠버의 기울기에 의한 받음각의 합으로 나타낼 수 있으며, 식으로 나타내면 다음과 같다. 

$$\alpha+\theta=\alpha+\tan^{-1}\left( -{dz\over dx} \right)$$

 

받음각이 작고 얇은 에어포일에 대해 다음과 같이 근사하여 식을 간단하게 만들 수 있다.

$$\alpha+\theta=\alpha+\tan^{-1}\left( -{dz\over dx} \right)=\alpha-{dz\over dx}$$

 

유동의 속도 $V_\infty$중 캠버선에 수직한 유동 속도 성분을 $V_{\infty,n}$라고 하자. 

 

위에서 계산한 사이각 계산과정과 삼각함수 공식을 사용하면 $V_{\infty,n}$을 쉽게 계산할 수 있다.

 

$$V_{\infty,n}=V_\infty \left( \alpha-{dz\over dx} \right)$$

 

 

얇은 에어포일을 위 그림처럼 다시 그려서 노란색의 얇은 선으로 표현되는 경우를 생각해보자.

 

노란 선은 곧 에어포일의 캠버선이 될 것이고, 파란 선은 곧 에어포일의 시위선(chord line)이 될 것이다.

 

에어포일을 아주 먼 곳에서 바라본다면 캠버선과 시위선이 일치하는 것처럼 보일 것이다.

 

그래서 와류면에 의해 캠버선에 생성된 유동을 시위선에 생성된 유동으로 봐도 큰 차이는 없을 것이다.

 

즉, 에어포일의 경로 $s$ 대신 x축 좌표를 사용해도 무방하다는 것이다. 이를 식으로 나타내면,

$$w'(s)\sim w(x)$$

 

다시 설명하자면

1. 얇은 에어포일의 위치는 에어포일의 캠버선으로 그대로 사용하되

2. 각 위치에서 와류면을 고려할 때는 x축에 대응시켜 계산할 것이다. 

 

 

 

 

위 그림처럼 에어포일의 시위선이 x축을 따라 있는 경우를 생각해보자.

 

위에서 볼 수 있듯이, 변수 $x$와 $\xi$ 모두 x축을 따라 변하는 변수들이다.

 

이제 시위선 위의 요소 길이 $d\xi$에 의해 순환(circulation) $\Gamma=\gamma d\xi$ 가 발생할 것이다.

 

이때 $\gamma$는 단위길이당 와류면의 세기이고, $\xi$에 따라 변하는 양이므로 순환을 다음과 같이 다시 쓸 수 있다.

$$\Gamma=\gamma d\xi=\gamma (\xi) d\xi$$

 

이제 요소 길이 $d\xi$에 의해 생성된 순환이 있을 것이고, 이 순환에 의한 유동의 속도가 있을 것이므로, 임의 지점 $x$에서의 유동의 속도를 계산해보자.

 

$$dw=-{\gamma (\xi) d\xi\over 2\pi (x-\xi)}$$

 

위에서 계산한 값은 요소 길이 $d\xi$에 의한 것이므로 시위선을 따라 모든 요소에 대해 적분한다면 $x$에서 유도되는 총 유동 속도가 계산된다.

 

$$w(x)=-\int_0^c {\gamma (\xi) d\xi\over 2\pi (x-\xi)}$$

 

위 그림에 대해 다시 생각해보자.

 

유동이 에어포일 주변에서 흐를 때 에어포일의 바로 위와 바로 아래에서는 에어포일과 평행한 방향으로 흐른다.

 

이것은 곧 에어포일에서 에어포일에 수직한 방향의 유동 속도는 0이라는 의미이고, 이는 유동이 에어포일을 뚫고 지나가지 못한다는 말과 같다.

 

위의 조건을 식으로 표현하면 다음과 같다.

$$V_{\infty,n}+w'(s)=0 \\ V_\infty \left( \alpha-{dz\over dx} \right)-\int_0^c {\gamma (\xi) d\xi\over 2\pi (x-\xi)}=0$$

 

위 식이 얇은 에어포일 이론의 기본 방정식이다.

 

 

대칭형 에어포일(Symmetric airfoil)

 

에어포일이 x축에 대해 대칭을 이룰 때의 경우를 이미 살펴본 얇은 에어포일 이론의 기본 방정식으로부터 유도해보자.

 

대칭형 에어포일의 경우 x축을 따라 캠버가 존재하므로 항상 (${dz\over dx}=0$)을 만족한다. 

 

따라서 기본 방정식은 다음과 같이 변한다.

$$ V_\infty \left( \alpha-{dz\over dx} \right)-\int_0^c {\gamma (\xi) d\xi\over 2\pi (x-\xi)}=0 \\ V_\infty \alpha = {1\over 2\pi} \int_0^c  {\gamma (\xi) d\xi\over x-\xi}$$

 

식이 훨씬 간단해졌으므로, 이제 위 식의 해를 직접 계산할 수 있다.

 

먼저 $\xi$를 $\theta$에 대한 식으로 치환하자.

$$\xi={c\over 2}(1-\cos\theta)$$

 

위와 같은 변환을 특정 위치 $x$에 대해 적용했을 때의 $\theta$를 $\theta_0$이라고 한다면 다음 식이 성립한다.

$${1\over 2\pi}\int_0^\pi {\gamma (\theta) \sin\theta d\theta \over \cos\theta - \cos\theta_0} = V_\infty \alpha$$

 

위 식에 대한 해는 다음과 같이 주어진다. 자세한 풀이과정은 너무 어려우므로,,,, 패쓰,,,,

$$\gamma (\theta) = 2\alpha V_\infty {1+\cos\theta\over\sin\theta}$$

 

 

이제 양력 계수를 계산하기 위해 에어포일 주위의 전체 순환을 계산해보자.

$$\Gamma=\int_0^c {\gamma (\xi) d\xi} \\ \Gamma={c\over 2} \int_0^\pi {\gamma (\theta) \sin\theta d\theta}$$

위에서 구한 해를 대입하면,

$$\Gamma=\alpha c V_\infty \int_0^\pi (1+\cos\theta)d\theta=\pi\alpha c V_\infty$$

 

에어포일의 전체 순환을 알고 있으므로, 에어포일의 단위 스팬당 양력을 Kutta-Joukowski 이론에 의해 다음과 같이 구할 수 있다.

$$L'=\rho_\infty V_\infty \Gamma = \pi\alpha c \rho_\infty V_\infty^2$$

 

이제 에어포일의 양력 계수를 정의에 의해 다음과 같이 구할 수 있다.

$$c_l={L'\over q_\infty S}$$

 

여기서 $S=c(1)$이므로,

$$c_l={\pi\alpha c \rho_\infty V_\infty^2\over{1\over 2}\rho_\infty V_\infty^2 c} \\ c_l=2\pi\alpha \\ {d c_l \over d\alpha}=2\pi$$

 

위 식을 통해 양력 곡선(양력 계수-받음각 그래프)의 기울기는 항상 $2\pi$임을 알 수 있었다.

 

 

대칭형 에어포일에서 앞전에 대한 모멘트 계산

 

이제 Kutta-Joukowski 이론을 이용해서 앞전에 대한 에어포일의 모멘트를 계산해보자.

 

 

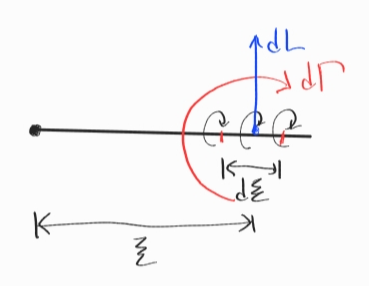
왼쪽 끝이 앞전이고, 에어포일의 임의 요소의 위치를 $\xi$, 길이를 $d\xi$로 표현하면 위 그림처럼 나타낼 수 있을 것이다.

 

각 요소의 순환은 다음과 같이 계산할 수 있다.

$$d\Gamma = \gamma (\xi)d\xi$$

 

그렇다면 Kutta-Joukowski 이론에 의해, 요소의 양력은 다음과 같다.

$$dL=\rho_\infty V_\infty d\Gamma=\rho_\infty V_\infty \gamma (\xi)d\xi$$

 

요소에 작용하는 양력과 요소의 위치를 곱함으로써, 요소에 의한 앞전에 대한 모멘트를 구할 수 있다.

$$dM=-\xi (dL)$$

(에어포일에서 모멘트 방향은 시계방향이 (+) 방향인 것을 잊지 말자!)

 

적분을 통해 앞전에 대한 모멘트를 구해보면,

$$M_{LE}'=-\int_0^c \xi (dL) = -\rho_\infty V_\infty \int_0^c \xi \gamma (\xi) d\xi \\ M_{LE}'=-q_\infty c^2 {\pi\alpha \over 2}$$

 

모멘트 계수의 정의에 의해 모멘트 계수를 계산해보면,

$$c_{m,LE}= {M_{LE}'\over q_\infty c^2}=-{\pi\alpha\over 2}$$

 

그런데 양력 계수를 위에서 $c_l=2\pi\alpha$라고 구했으므로 이를 대입해보자.

$$c_{m,LE}= -{c_l\over 4}$$

 

앞전에 대한 모멘트와 양력 계수를 이용해서 다음과 같이 1/4 시위점에 대한 모멘트를 계산할 수 있으므로, (FBD를 그려 간단히 확인할 수 있다.)

$$c_{m,c/4}=c_{m,LE}+{c_l\over 4}=0$$

 

위 식을 통해 1/4 시위점에서 모멘트 값이 0이 됨을 알았다. 

 

따라서 압력 중심의 정의에 의해 대칭형 익형에서는 압력 중심이 1/4 시위점에 존재한다는 사실을 알게 됐다! 

 

심지어 압력 중심의 위치가 받음각에 영향을 받지 않으므로 1/4 시위점은 압력 중심인 동시에 공력 중심이기도 하다.