항공역학 [14] 에어포일 주위의 비압축성 유동 - 와류면, Kutta 조건(Vortex sheet, Kutta condition)

와류면(Vortex sheet): 에어포일 주위 유동에 대한 이론적 해

 

와류 유동(Vortex flow)에 관한 글에서 와류가 무엇인지, 어떻게 표현되는지에 대해 설명했다.

앞서 다뤘던 와류 유동의 경우 2차원 유동에 대해서만 생각해 봤었다. 

 

이번 글에서는 3차원 공간에서의 와류 유동에 대해 생각해보자.

공간에 와류 필라멘트(Vortex filament)라고 불리는 얇은 직선이 존재하고, 와류 필라멘트 위의 모든 점에서 와류 유동은 모두 동일하다고 가정하자.

 

이를 그림으로 표현하면 다음과 같을 것이다.

다시 생각해보면, 와류 필라멘트와 수직한 면으로 잘랐을 때 보이는 부분이 바로 와류 유동인 것이다.

 

점(와류 유동)을 쌓아 선(와류 필라멘트)을 만들었으니, 이제 선(와류 필라멘트)을 쌓아 면(와류면)을 만들어볼 것이다.

그림으로 표현하면 다음과 같다.

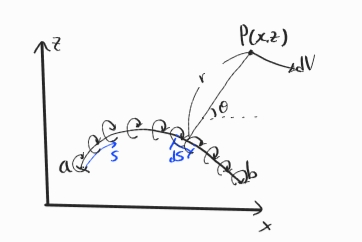
와류 필라멘트가 y축 방향으로 뻗어있다고 할 때, xz평면에 대해 그린 것이다.

 

a부터 b까지의 선이 바로 와류면을 의미하며, 선 위의 각 점은 y축 방향으로 뻗어있는 와류 필라멘트를 의미한다. 

 

와류 유동에서 속도를 계산하는 방법을 사용해 임의의 점 P에서의 속도 $\mathbf{V}$를 구해보자.

위 문제의 경우 단위 길이당 와류면의 강도를 $\gamma$라고 정의할 것이다. 

 

먼저 a부터 b까지의 선 중 요소 길이 $dS$에 의해 점 P에 유도되는 요소 속도를 $\mathbf{dV}$라고 하자.

 

와류면 $dS$의 강도는 $\gamma dS$이므로, 와류 유동에서 구하는 속도 공식에 의해 요소 속도 $\mathbf{dV}$는 다음과 같이 구할 수 있다.

$$\mathbf{dV}=-{\gamma dS \over 2\pi r}$$

 

그렇다면 전체 와류면에 의해 점 P에서 생기는 속도 $\mathbf{V}$는 다음과 같이 적분을 통해 구할 수 있다.

$$\mathbf{V}=\int_a^b \mathbf{dV}=-\int_a^b {\gamma \over 2\pi r}dS$$

 

위에서 유동의 속도를 구했으므로, 다음 식을 이용해 속도 퍼텐셜 $\phi$의 증분 $d\phi$를 계산할 수 있다.

$${1\over r}{\partial \phi \over\partial \theta}=V_\theta=-{\gamma dS\over 2\pi r} \\ {\partial \phi \over\partial \theta}=-{\gamma dS\over 2\pi} \\ d\theta=-{\gamma dS\over 2\pi}\theta$$

 

전체 와류면에 대해 적분하면, 다음과 같이 점 P에서의 속도 퍼텐셜을 계산할 수 있다.

$$\phi(x,z)=-{1\over 2\pi}\int_a^b \theta\gamma dS$$

 

와류면 주위 순환(circulation)은 요소 길이에 대한 요소 와류 강도를 적분함으로써 얻을 수 있고, 그것을 식으로 나타내면 다음과 같다.

$$\Gamma=\int_a^b \gamma dS$$

 

이렇게 계산한 순환 값을 활용해 에어포일의 양력을 계산할 수 있다.

Kutta-Joukowski 정리에 의해,

$$L'=\rho_\infty V_\infty \Gamma$$

 

 

Kutta 조건(Kutta condition)

 

에어포일 주위의 유동 흐름을 생각해보자.

만약 에어포일의 뒷전이 뾰족하고, 유동이 뒷전을 돌아 지나가는 상황을 가정하자.

아래 식에 의해 같은 순환 $\Gamma$에 대해 뒷전의 모서리가 날카로울수록($r\to 0$) 뒷전에서의 속도가 빨라질 것($V_\theta \to \infty$)이다.

$$V_\theta=-{\Gamma\over 2\pi r}$$

 

자연계에서 무한대의 속도를 가지는 유동은 존재할 수 없으므로 뒷전에서의 유동을 설명하기 위한 적절한 해결책을 찾아야한다.

 

뒷전에서의 각도가 유한한 경우와, 뒷전에서의 각도가 0에 수렴하는 경우를 나누어 생각해보자.

먼저 유한각 뒷전의 경우를 살펴보자. 검정색 선이 에어포일의 뒷전 부분이고, 파란색 화살표가 유동의 속도를 의미한다.

 

뒷전에서 윗면을 따라 흐르는 속도를 $\mathbf{V}_1$, 아랫면을 따라 흐르는 속도를 $\mathbf{V}_2$라고 하자.

 

이러한 속도들이 한 점(뒷전)에서 유한한 값을 갖는다는 것은, 유동이 한 점에서 방향이 다른 두 개의 속도를 동시에 갖는다는 말과 같다.

이것은 당연하게도 물리적으로 불가능하며, 이를 해결하는 유일한 방법은 $\mathbf{V}_1$과$\mathbf{V}_2$를 모두 0으로 만드는 것이다. 

 

정체점(Stagnation point)의 정의에 따라, 에어포일의 앞부분에서처럼 에어포일의 뒷전도 정체점이 될 것이다.

 

이번에는 아주 날카로운 뒷전의 경우를 살펴보자. (뒷전에서 윗면과 아랫면이 이루는 각도가 거의 0)

 

위에서 정의한 것과 같이, 유동이 뒷전에서 윗면을 따라 흐르는 속도를 $\mathbf{V}_1$, 아랫면을 따라 흐르는 속도를 $\mathbf{V}_2$라고 하자.

 

$\mathbf{V}_1$과 $\mathbf{V}_2$가 이루는 각도가 0이므로, $\mathbf{V}_1$과 $\mathbf{V}_2$는 같은 방향을 갖는다고 할 수 있다. 

 

우리가 살펴보는 것은 비점성, 비압축성 유동이므로 유동 내 모든 점에서 베르누이 방정식(Bernoulli Equation)이 성립한다는 것을 이용하면 $\mathbf{V}_1$과 $\mathbf{V}_2$는 같다는 것을 쉽게 보일 수 있을 것이다.

 

뒷전이 유한각을 가지는 경우와 아주 날카로운 경우 모두 뒷전에서 생성되는 와류가 없으므로, 뒷전에서의 와류면의 세기 $\gamma$는 0이 된다.

 

 

따라서 에어포일 주위에 유동이 흐를 때, 익형 주위의 순환 $\Gamma$는 뒷전에서 유동이 매끄럽게 빠져나가도록 하는 값을 갖는다는 것이 Kutta 조건이며, 구체적인 사항은 다음과 같다.

 

1. 뒷전이 유한한 각을 가질 경우 뒷전은 정체점이다.

2. 뒷전이 아주 날카로울 때 윗면과 아랫면에서의 유동의 속도는 방향과 크기가 같다.

 

 Kutta 조건을 와류면의 세기에 대해 표현하면 '뒷전에서의 와류면의 세기는 0'이므로 이를 식으로 나타내면 다음과 같다.

$$\gamma(TE)=0$$