전자기학[4] 정전기장-정전기장 내의 도체

물질은 전기적 특성에 따라 세 가지로 나눌 수 있는데, 도체(Conductor), 반도체(Semiconductor), 부도체(절연체, Insulator)로 각각 나눌 수 있다. '전기 전도도'에 따라 구분한 것인데, 고등학교 수준에서는 부도체에서 도체로 갈수록 원자 사이를 자유롭게 오갈 수 있는 자유전자가 많아져 전기 전도도가 높아진다고만 이해하면 쉽다. 전기 전도도는 전기 저항의 역수로 정의되며, 전기를 얼마나 잘 흐르게 하는지를 나타내는 물리량이다. 일반적으로 전기전도도가 $10^6 S/m$(흑연(C)의 전기전도도) 보다 크면 도체, 전기 전도도가 $10^{-6}S/m$이하이면 부도체, 그 사이면 반도체라고 본다.

조금 더 엄밀히 구분하자면 Band Theory(띠구조 이론)로 설명할 수 있다. Band Theory에 의하면, 전자가 가질 수 있는 에너지는 제한적이며 전자가 존재할 수 있는 에너지 영역을 에너지 띠(Energy band)라고 한다. 반대로 전자가 가질 수 없는 에너지 영역은 Bandgap(Energy gap, 밴드갭, 에너지 갭)라고 한다. 단순한 그림으로 설명하면 다음과 같다.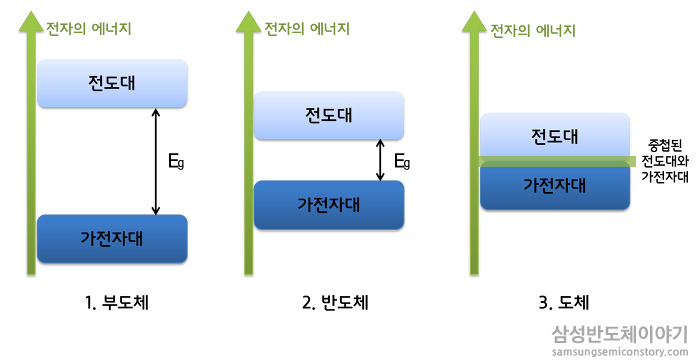

출처: 삼성반도체이야기

이온화되지 않은, 즉 양성자의 개수와 전자의 개수가 같은 상태인, 즉 안정적인 원자에서 전자의 에너지 상태가 존재하는 밴드를 Valence Band(가전자대)라고 한다. 반대로 Conduction Band(전도대)는 Valence Band에 있던 전자가 에너지를 얻어 들뜬상태가 되었을 때 올라갈 수 있는 에너지 밴드를 뜻한다. Conduction Band에 있는 전자들만이 물질에 전류가 흐르게 할 수 있다고 보면 된다. 이 두 Band 사이의 차이가 Band gap이 된다. 

위 그림에서 볼 수 있듯 부도체에서는 밴드갭이 너무 커 Valence Band의 전자가 Conduction Band로 쉽게 올라가지 못해 전기가 잘 통하지 않는다고 생각하면 된다. 반대로 도체에서는 밴드갭이 없이 Valence Band와 Conduction Band가 중첩되어 물질을 이온화하지 않아도 전기가 잘 통하는 특징이 있다. 반도체는 물론 그 사이의 특성을 갖고 있다.

 

이야기가 조금 샜는데, 다시 전자기장 내의 도체 얘기로 돌아가 보자. 임의의 전하가 도체 내부에 존재한다고 가정한다면 도체에는 전기장이 형성되고, 그 전기장에 의해 각 전하에 밀어내는 힘이 인가된다. 이 힘은 전하를 도체 표면까지 밀려나도록 하며, 평형상태에 이르게 되면 도체 내부에는 전하와 전기장이 존재하지 않게 된다.

평형 상태의 도체 표면에서 전기장 $E$가 존재한다면 전하가 전기장에 의해 움직이게 되므로 정전기장의 조건에 부합하지 않는다. 따라서 정전기장에서는 전기장 $E$가 도체 표면에서 수직 방향으로만 존재해야 한다. 이는 도체 표면이 항상 등전위면임을 의미한다.

 

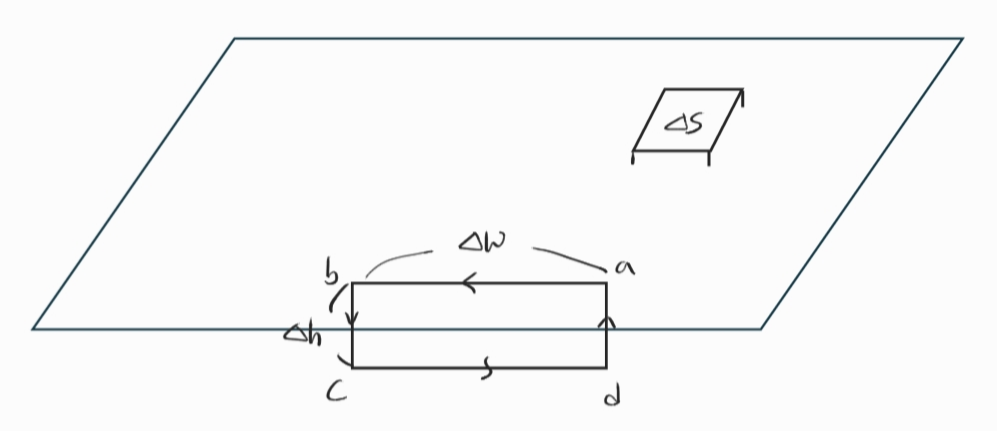
위의 그림의 1번 루프를 돌며 전기장 벡터를 선적분 해보자. 가우스 정리에서 보인 것과 같이 $\int_L E\cdot dl=0$을 적용한다면 다음과 같은 결과를 얻을 수 있다.

$$\oint_{abcda} E\cdot dl=\int_{cd} 0 \cdot dl+\left( \int_{bc} E_n \cdot dl+\int_{da} E_n \cdot dl \right)+\int_{ab} E_t \cdot dl$$

괄호로 묶인 부분은 크기가 같고 방향이 반대이므로 합이 0이 되고, cd는 도체 내부에 있으므로 $E_t=0$이다. 따라서 경로 ab만 남으므로 경로 ab를 따라 적분한다면 $\int_{ab}E\cdot dl=E_t \Delta w=0$이 나온다. 따라서 $E_t=0$, 즉 도체 표면에서의 전기장의 접선(tangential) 성분은 0이 된다는 것을 알 수 있다.

 

전기장의 수직 성분을 구하기 위해 $\Delta S$만큼의 상자를 설정하고 가우스 법칙을 적용하면 다음과 같은 결과가 나온다.

$$\oint_S E\cdot ds=E_n\Delta S = \frac{\rho_s \Delta S}{\epsilon_0}$$

따라서 $E_n=\frac {\rho_s} {\epsilon_0}$, 즉 도체 표면에서의 전기장의 법선(normal) 성분은 도체 표면의 면전하밀도를 진공의 유전율로 나눈 값과 같다는 것을 알 수 있다.

 

정리

자유공간 내에 있는 도체 표면에서의 경계조건
접선(tangential) 방향	$E_t=0$
법선(normal)방향	$E_n=\frac {\rho_s} {\epsilon_0}$