항공역학 [10] 비압축성 유동 분석 (1) - 속도 조건, 경계 조건(Velocity condition, Boundary condition)

비압축성 유동의 속도 조건

이번 파트에서 다룰 비압축성(Incompressible) 유동은 말 그대로 유체가 압축되지 않는다는 가정을 전제로 하고 있다.

연속 방정식에 관한 글에서 살펴본 식부터 출발하여, 속도에 관한 조건이 무엇이 있는지 살펴보자.

$${\partial\rho\over\partial t}+\nabla\cdot\rho\mathbf{V}=0$$

위 식에서 주목해야 할 점은 비압축성 유동에서 밀도 $\rho$가 시간에 따라 변하지 않는다는 점이다.

따라서 ${\partial\rho\over\partial t}=0$이므로,

$$\nabla\cdot\rho\mathbf{V}=0\\\rho(\nabla\cdot\mathbf{V})=0\\\nabla\cdot\mathbf{V}=0$$

 

지배 방정식: 라플라스 방정식(Laplace's Equation)

속도 퍼텐셜에 관한 글에서 속도를 속도 퍼텐셜(Velocity Potential) $\phi$로 나타내는 방법을 다뤘었다. 

위에서 구한 속도 조건과 속도 퍼텐셜 $\phi$를 이용해 새로운 방정식을 유도해보자.

$$\nabla\cdot\mathbf{V}=0$$

이때 $\mathbf{V}=\nabla\phi$ 이므로,

$$\nabla\cdot (\nabla\phi)=0 \\ \nabla ^2 \phi=0$$

위 식은 라플라스 방정식의 형태이며, 공학 전반에서 많이 나오는 방정식 형태이다.

(심지어 전자기학 글 중 벡터 자기장 포텐셜에 관한 글에서도 등장한다!)

 

이렇게 유도된 라플라스 방정식을 보기 쉽도록 여러 좌표계에 대해 정리해보자.

-직교 좌표계(Orthogonal Coordinate)

$$\nabla ^2 \phi={\partial^2\phi\over\partial x^2}+{\partial^2\phi\over\partial y^2}+{\partial^2\phi\over\partial z^2}=0$$

-원통형 좌표계(Cylinderical Coordinate)

$$\nabla ^2 \phi={1\over r}{\partial\over\partial r} \left( r {\partial\phi\over\partial r}\right)+{1\over r^2}{\partial^2\phi\over\partial \theta^2}+{\partial^2\phi\over\partial z^2}=0$$

 

 

무한대 경계 조건(Infinity Boundary Condition)

유동 내의 물체로부터 무한히 먼 곳에 대한 조건에 대해 알아보자.

유체가 x축을 따라 흐른다고 가정하자.

물체에서 가까운 부분에서는 유동이 물체의 존재로 인한 영향을 받아 원래의 유동 상태인 자유 유동(Free stream)과는 상당히 다른 양상을 보일 것이다. 

그런데 물체에서 굉장히 먼 곳에서는 물체의 존재가 유동의 상태에 미치는 영향이 아주 작을 것이다.

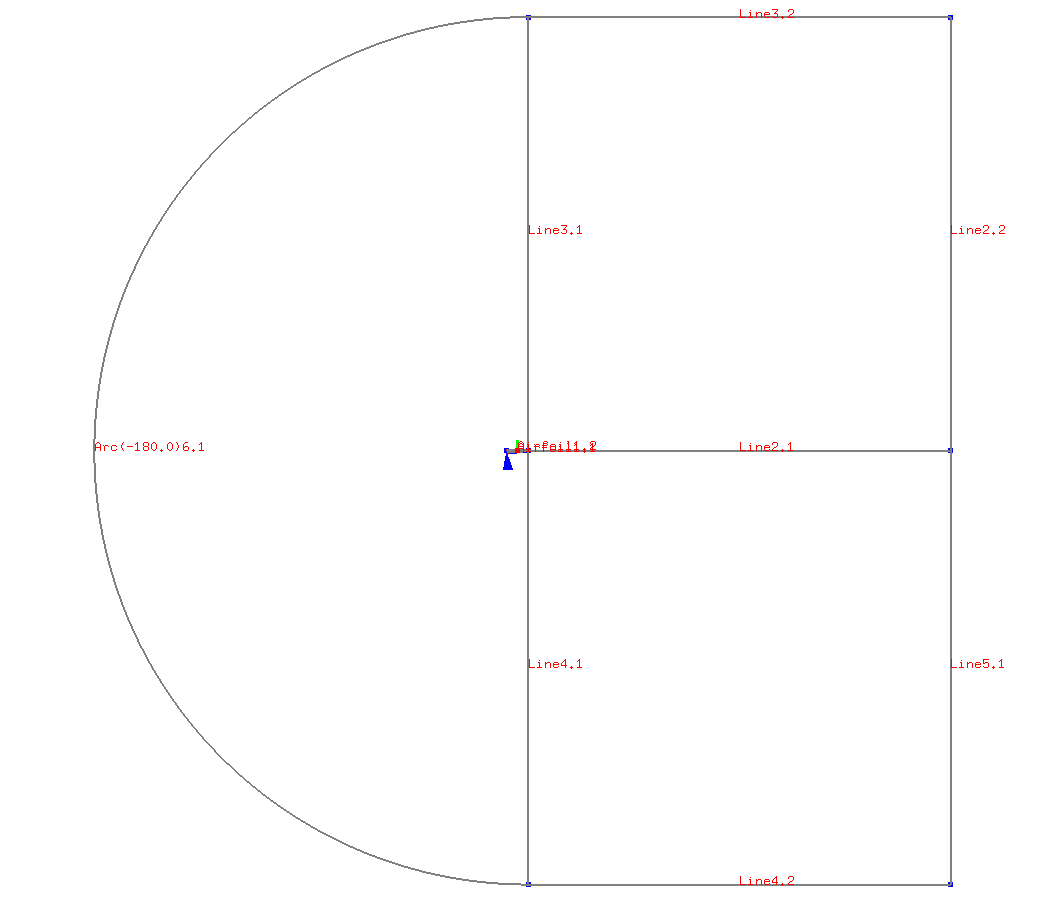
무한대 경계 예시: 파란 화살표 위치에 에어포일이 있어요!

따라서 물체로부터 매우 멀리 떨어진 곳에서의 유동은 자유 유동의 상태로 여겨지며, x축 방향과 평행한 방향으로 흐른다.$(u=V_\infty, v=0)$

$$u={\partial\phi\over\partial x}={\partial\psi\over\partial y}=V_\infty \\ v={\partial\phi\over\partial y}=-{\partial\psi\over\partial x}=0$$

 

벽면 경계 조건(Wall Boundary Condition)

유동 속 물체가 고체 표면을 갖고 있다면, 유체가 고체 표면을 통과하지 못한다는 것은 너무나 당연한 사실이다. 

다시 말해, 물체의 표면에서 유동의 속도 벡터 방향은 물체 표면의 접선(tangential) 방향이어야 하고, 동시에 물체 표면의 법선(normal) 방향과 수직이어야 한다.

물체 표면의 법선 방향 단위 벡터를 $\mathbf{n}$이라고 하면, 아래 식이 성립한다.

$$\mathbf{V}\cdot\mathbf{n}=(\nabla\phi)\cdot\mathbf{n}=0$$

 

위 식을 속도 포텐셜 및 유선 함수에 관한 식으로 나타내면 아래와 같다. (이때 $s$의 방향은 $n$의 방향과 수직인 방향, 즉 물체 표면의 접선 방향과 평행한 방향이다.)

$${\partial\phi\over\partial n}=0 \\ {\partial\psi\over\partial s}=0$$

 

두 번째 식인 유선 함수에 관한 식을 보면 흥미로운데, 두 번째 식은 유선 함수는 물체의 표면을 따라 변화량이 0이라는 뜻이다.

즉, 물체의 표면이 곧 유동의 유선이라는 것을 의미한다!