전자기학[11] 정상상태 전류 - 키르히호프의 전압법칙

앞선 글에서 정전기장을 설명할 때 정전기장 $E$를 임의의 폐경로(closed loop)를 따라 선적분을 수행하면 그 값이 0이 됨을 확인했다. 식으로 나타내면 다음과 같다.

$$\oint_C E\cdot dl=0$$

여기서 저항성 매질의 특징인 $J=\sigma E$를 이용하여 위 식을 다시 쓰면 다음 식과 같다.

$$\oint_C {1\over\sigma} J\cdot dl=0$$

 

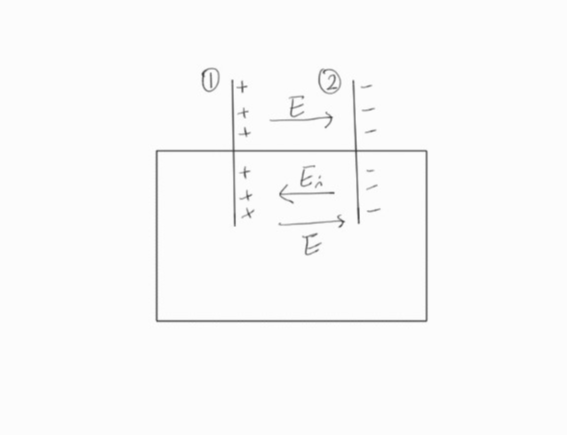
위 그림처럼 2개의 전극을 갖는 전지를 고려하자. 전지 내의 화학적 작용으로 인해 1번 전극에는 양전하가, 2번 전극에는 음전하가 축적된다. 이러한 전하들은 전지의 안쪽과 바깥쪽에 모두 $E$의 전기장을 발생시킨다. 

그런데 위의 그림에서 알 수 있듯이 위 회로는 개방된 상태이며, 전지에는 전류가 흐르지 않으며, 따라서 전지 내부의 전하에 작용하는 힘(net force)는 0이다. 따라서 전지 내부에서는 쌓인 전하에 의한 정전기장 $E$와 균형을 이루는, 즉 크기는 같고 방향이 정반대인 화학작용에 의해 비보존력 $E_i$이 발생되는 것을 알 수 있다. $E_i$는 인가된 전기장 세기(impressed electric field intensity)라고 하며, 이를 전지 내부의 음극에서 양극까지 선적분한 값을 전지의 기전력(electromotive force 또는 electromotance)(emf)라고 부른다. 기전력의 단위는 볼트(volt)이며, 1800년에 화학전지를 발명한 알렉산드로 볼타의 이름에서 유래했다고 한다. 참고로 기전력의 '력'은 힘을 나타내는 力을 사용하지만, 사실 물리학의 힘(Force, N)와는 전혀 관계가 없다. 

 

기전력에 정의의 의해 다음과 같은 식을 쓸 수 있다.

$$V=\int_2^1 E_i \cdot dl=-\int_{2}^1 E\cdot dl(\text{전지 안쪽})$$

 

폐회로에 대해 정전기장 세기$E$를 선적분한 값은 0이므로 다음과 같은 식이 성립한다.

$$\oint_C E\cdot dl=\int_1^2 E\cdot dl(\text{전지 바깥쪽})+\int_2^1 E\cdot dl(\text{전지 안쪽})=0$$

위 식과 기전력에 관한 식을 결합하면 아래 식이 성립한다.

$$V=\int_1^2 E\cdot dl=V_1-V_2$$

 

기전력(emf)는 전지 내부에서의 전압 상승이라고 해석하기도 한다.

 

전지와 같은 비보존력이 폐회로에 존재할 경우, 다음과 같은 적분식이 성립한다.

$$V=\oint_C J\cdot dl=RI$$

 

폐회로에 하나 이상의 기전력과 하나 이상의 저항이 있는 경우는 위 식을 일반화하여 다음과 같이 나타낼 수 있다.

$$\sum_j V_j=\sum_k R_k I_k \quad (V)$$

이는 전기회로에서 폐경로에 대한 기전력(전압 상승)의 합은 그 경로에 존재하는 저항에 의한 전압강하의 합과 같다는 것을 의미하며, 키르히호프의 전압법칙(Kirchhoff's Voltage Law, KVL)를 나타내는 식이다.

임의의 폐경로에 대해 모두 적용할 수 있고, 선적분 경로의 방향도 임의로 정할 수 있다.