전자기학[24] 맥스웰 방정식 - 시간에 따라 변하는 전자기장 (1)

드디어 전기장과 자기장이 시간에 따라 변할 때에 대해 공부할 수 있게 되었다.

과거에는 전기와 자기가 전혀 관계 없는 것으로 생각되어 전기장과 자기장에 대해 각각 따로 공부했지만, 그 유명한 페러데이(Michael Faraday)와 다른 과학자들의 많은 실험을 통해 전기와 자기는 상관관계가 있다는 것을 알게 되었다.

전기장이 시간에 따라 변할 때 자기장이 형성되고, 반대로 자기장이 시간에 따라 변할 때 전기장이 형성된다는 것이다!

실험을 통해 서로 관계가 있다는 것은 알았고, 구체적으로 생각하고 자세히 정의해보자.

 

시간에 따라 변하지 않는(시불변, time invarient) 전자기장 (정전기장/정자기장)

 

우리는 이미 앞선 23개의 글을 통해 시간에 따라 변하지 않는 전자기장에 대해 알아보았다.

전기장 세기 벡터 $\mathbf{E}$, 전속밀도 벡터 $\mathbf{D}$를 통해 정전기장을 표현했고 자기장 세기 벡터 $\mathbf{H}$, 자속밀도 벡터 $\mathbf{B}$를 통해 정자기장을 표현했다.

 

정전기장과 정자기장에서 각각의 관계는 다음 표와 같이 정리할 수 있다.

 

정전기장	정자기장
$\nabla \times \mathbf{E}=0$	$\nabla \cdot \mathbf{B}=0$
$\nabla \cdot \mathbf{D}=\rho$	$\nabla \times \mathbf{H}=\mathbf{J}$
$\mathbf{D}=\epsilon\mathbf{E}$	$\mathbf{H}={1\over\mu}\mathbf{B}$

위의 표처럼 시간에 따라 변하지 않는 정상상태(steady state)에 있는 상태에서는 전기장과 자기장이 서로 영향을 끼치지 않는다. 

하지만 시간에 따라 전기장/자기장이 변할 때 자기장/전기장이 형성되는 것을 실험을 통해 밝혔고, 이를 수식으로 표현한 것이 그렇게 유명한 맥스웰 방정식(Maxwell's Equation)이다. 

 

전자기 유도 현상에 관한 패러데이 법칙, 렌츠의 법칙

 

1831년 마이클 패러데이(Michael Faraday)는 폐루프에 걸리는 쇄교자속(결합자속, magnetic flux linkage)의 크기가 변하면 폐루프에 전류가 유도되는 것을 발견했다. 쉽게 다시 말하자면, 전선을 동그랗게 이어놓고 그 사이에 자석을 통과시키면 전선에 전류가 흐른다는 것이다. 

이런 결합자속의 변화와 유도되는 기전력의 상관관계를 나타내는 것이 패러데이의 법칙(Faraday's Law)이다. 

 

이번에도 아래와 같은 기본 가정을 통해 전자기 유도 현상에 대해 설명해 보겠다. 

$$\nabla \times \mathbf{E}=-{\partial \mathbf{B} \over \partial t}$$

 

임의의 면적에 대해 위 식 양변을 적분하고, 좌변에 스토크스의 정리를 적용해 다시 쓰면 아래와 같이 나타낼 수 있다.

$$\oint_C \mathbf{E}\cdot dl=-\int_S {\partial \mathbf{B}\over \partial t}\cdot ds$$

이 때 $S$는 임의의 면적을 의미하고, $C$는 $S$를 둘러싸는 경로를 의미한다.

 

적분을 행하는 면적이 시간에 따라 변하지 않고 일정하다면, 시간에 대한 미분항을 적분기호 밖으로 꺼낼 수 있으므로 아래와 같이 쓸 수 있다.

$$\oint_C \mathbf{E}\cdot dl=-{d \over dt}\int_S \mathbf{B}\cdot ds$$

 

 

그런데 좌변을 잘 살펴보면 경로 $C$를 따라 전기장 세기 벡터를 선적분한 것이므로 루프 $C$에 유도된 기전력과 같고, 우변을 잘 살펴보면 면적 $S$를 수직으로 통과하는 자속과 같다는 것을 알 수 있다.

이를 식으로 나타내면 아래와 같다.

$$V=\oint_C \mathbf{E}\cdot dl \quad (V)\\ \Phi=\int_S \mathbf{B}\cdot ds \quad (Wb)$$

이 관계를 위의 식에 그대로 대입한다면 재밌는 결과가 나온다.

 

$$V=-{d\Phi \over dt}\quad (V)$$

위 식을 풀어 쓰자면 고정된(아까 면적이 시간에 따라 변하지 않는다는 가정을 했으므로) 폐루프에 유도되는 기전력은 그 루프를 관통하는 자속의 증가율에 음의 부호를 붙인 것과 같다는 의미이다. 

즉, 결합자속의 시간에 대한 변화를 방해하는 방향으로 유도기전력이 발생한다는 것인데, 이를 렌츠의 법칙(Lenz's law)라고 한다.

 

 

변압기(transformer)

 

변압기는 교류회로에서 전자기장의 원리를 이용해 간단히 전압, 전류, 임피던스를 조절할 수 있는 장치이다.

간단한 변압기의 구조는 아래의 그림처럼 생겼다. 강자성체로 이루어진 코어가 있고, 두 개 이상의 코일이 자기적으로 결합하여 자기회로를 구성하는 모습이다.

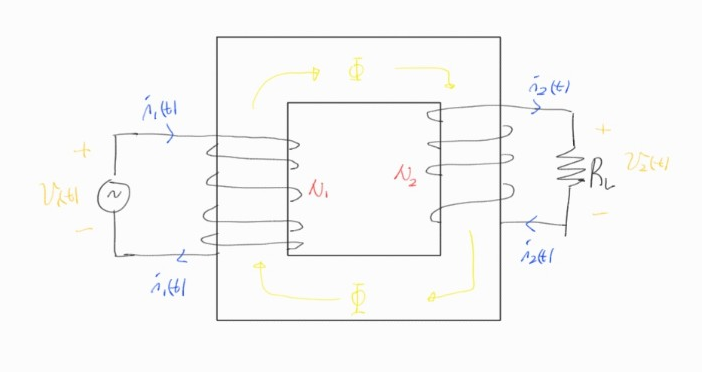
시간에 따라 변하는 값이므로 $v_1(t)$와 같이 표현했다.

자기회로에 관한 글에서 설명했듯이 전기회로와 비슷한 방법으로 자기회로에 대한 분석이 가능하다. 전압에 대응하는 기자력$(V_m=NI)$, 전류에 대응하는 자속$(\Phi)$, 저항에 대응하는 자기저항$(R_m)$을 통해 위 자기회로에 대해 키르히호프의 전압법칙을 적용해보면 아래와 같은 식을 유도할 수 있다.

$$V_m=N_1 i_1-N_2 i_2=\Phi R_m$$

 

위 식에서 자기저항은 코어로 사용한 강자성체에서 발생하는 손실로 인해 생기는데, 만약 손실이 없는 이상적인 변압기에서는 자기저항 값이 0이므로 위 식에서 우변의 값이 0이 된다. 따라서 아래의 식이 성립한다.

$${i_1 \over i_2}={N_2 \over N_1}$$

즉 1차측에 흐르는 전류와 2차측의 흐르는 전류의 비는 1차측의 권선수와 2차측의 권선수의 비의 역수와 같다는 것을 의미한다.

 

 

패러데이의 법칙을 통해 전압에 관한 아래의 두 식을 유도할 수 있다.

$$v_1=N_1{d\Phi \over dt}\\ v_2=N_2{d\Phi \over dt}$$

같은 강자성체를 이용해 자기적으로 결합되어 있으므로, 변압기의 1차측과 2차측의 시간에 따른 자속의 변화율은 같다. 따라서 아래의 식이 성립한다.

$${v_1 \over v_2}={N_1 \over N_2}$$

즉 1차측과 2차측의 전압비는 1차측과 2차측의 권선비와 동일하다는 것을 의미한다.

 

 

유효 부하저항, 유효 임피던스

 

위에서 사용한 그림처럼 1차측에는 교류전원, 2차측에는 부하(load)저항 $R_L$이 있는 경우를 가정해보자. 2차측에서관찰하는 부하저항 값은 당연히 $R_L$이다. 그렇다면 1차측에서 관찰하는(느끼는) 부하저항 값은 얼마일까?

 

부하저항 값은 2차측의 전압을 2차측의 전류로 나눔으로써 얻을 수 있다.

그리고 1차측의 유효 부하저항(1차측에서 관찰했을 때의 부하저항 값)은 1차측의 전압을 1차측의 전류로 나눠주면 구할수 있다. 

이상적인 변압기에서 1차측의 전압과 전류는 각각 2차측의 전압과 전류, 권선비로 나타낼 수 있다는 사실을 이용하여 1차측의 유효 부하저항을 구해보자.

$$R_1={v_1 \over i_1}={{N_1 \over N_2}v_2 \over {{N_2 \over N_1}i_2}}\\R_1=({N_1\over N_2})^2 R_L$$

 

이와 같은 방법으로 부하 임피던스 $Z_L$이 존재할 때, 권수비를 이용하여 1차측에 작용하는 유효 임피던스를 구할 수 있다.

$$Z_1=({N_1\over N_2})^2 Z_L$$